Transformation of
Stresses/Mohrís Circle
In a Nut Shell:† In-plane (xy-plane)
stresses at an arbitrary point in a structure consist of
normal stresses, σx and σy, †in both the x and y-directions, as well as
shearing stresses τxy and τyx.† The values of these stresses at an
arbitrary point change depending on direction.† i.e. The values from a single element
strain gage placed at a point on a structure will give different values
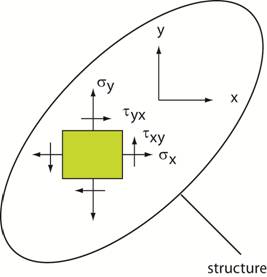
depending on the orientation of the gage. Sign Convention:† Consider a rectangular element taken from a
structure as shown in the
figure below.† The element depicts the
positive normal and shearing stresses on the element. ††† ††††††††††††††††††††† Terminology: †††††††††††††††††††††††† σ x =† normal component of stress in x-direction †††††††††††††††††††††††† σ y ††= normal component of stress in y-direction †††††††††††††††††††††††† τ xy †= shearing stress on the x-face in the y-direction †††††††††††††††††††††††† τ yx †= shearing stress on the y-face in the x-direction From
equilibrium it can be shown that†††† τxy†
=† τyx. Click
here to continue with discussion.† |
| Return to Notes on Solid Mechanics |
|---|
All rights reserved.
†
††††††††††††††††††††††