|
|
Key
Concepts: A
composite area is one that can be partitioned into a collection of known
areas such as rectangles, triangles, trapezoids, and circles as well as
voids of the same shapes. Voids are
taken as negative contributions.
|
|
In
a Nutshell: The
strategy to calculate the moment of inertia for a composite area is:
|
First |
Identify each part, its area, its centroid, and its centroidal
axes. |
|
Second |
Obtain the moment of inertia for each part (by
calculation or by table). |
|
Third |
Apply the parallel axis theorem if needed to
transfer from the centroidal
axes to the desired parallel axes. |
|
Fourth |
Sum the contribution for each individual part
as shown in the table below. |
|
Calculation
of Areas, First Moment, and Moments of Inertia
|
Area, A |
A = Σ
Ai = A1 ± A2 ± A3
± . . . . |
|
First Moment
ybar A |
ybar A
= y1bar A1 ± y2bar A2 ± y3bar
A3 ± . . . . |
|
Second Moment,
Iyy |
Iyy =
Iyy1 ± Iyy2 ± Iyy3 ± .
. . . |
|
Second Moment,
Izz |
Izz =
Izz1 ± Izz2 ± Izz3 ± .
. . . |
|
Polar Moment,
IP |
IP
= IP1 ± IP2
± IP3 ± . . . . |
|
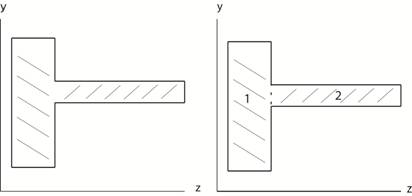
Note
the negative signs appearing in the table above apply with voids. As an example, the
cross-hatched composite area on the left can be
partitioned into two separate rectangular areas designated as 1 and 2 in
the figure on the right. Another
option would be to consider a large rectangular area encompassing 1 and 2
and then subtract rectangles above and below 2.
|
Click here for an example.
|