|
|
Key
Concepts: A pressure vessel is
generally a "thin˗walled"
structure (the ratio of radius to thickness
is large) subject to internal pressure,
p. The pressure produces normal
stresses
in
the plane of the structure which are determined from equilibrium of an
element.
|
In a Nut Shell: Thin-walled
pressure vessels store and transport gases or liquids under
pressure
such as pipelines, water towers, silos, and tanks. For example, compressors store air pressure
in tanks used at gas stations for tire inflation. Pressure vessels include:
|
Spherical Pressure Vessels |
|
Cylindrical
Pressure Vessels |
|
Capped
Pressure Vessels – Cylinder capped at each end by a hemisphere |
If r
is the inner radius of the sphere or cylinder and t is
the wall thickness, then the
sphere or cylinder is considered to be “thin” provided r/t
≥ 10.
First consider the case of
a thin-walled spherical pressure vessel with wall thickness, t,
internal radius, r, and internal pressure, p, as shown below.
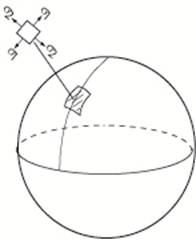
where
σ1, σ2 are the normal stresses on the outer
surface in (lb/in2), (lb/ft2), (N/mm2), (N/m2)
p is the internal pressure in (lb/in2), (lb/ft2),
(N/mm2), (N/m2)
r
is the internal radius of the spherical pressure vessel in (in), (mm),
etc
t
is the wall thickness of the spherical pressure vessel in (in), (mm),
etc
Note: The normal stresses, σ1 and
σ2 are the same in any
direction tangent to the outer
surface and constant throughout the thickness. They are the principal stresses at every
point.
Click
here to continue with discussion of a thin-walled, cylindrical pressure
vessel. |
