Composite
Beams
|
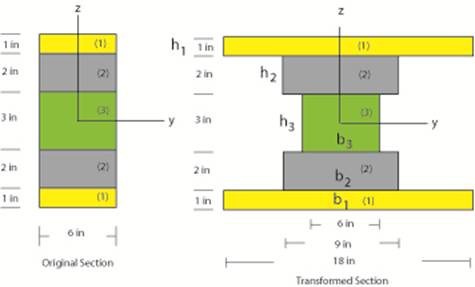
*Example: The original composite
beam shown on the left below is formed from three different materials with moduli of elasticity, E1, E2, and E3. The bending moment in the beam is to be 100,000 lb in and
E1 = 30x106 psi,
E2 = 15x106 psi, and E3 = 10x106
psi. Find the maximum bending
stress in each material of the composite beam.
|
|
1.
Select material (3) to be the
“base material”. Therefore E1 / E3 = 3
and E2 / E3 = 1.5.
Note: Any one material can be
selected as the “base material”. 2.
Form the “transformed section” using only the “base material” by
multiplying the width of section (2)
by 1.5 and the width of section 1 by 3.
The width of the base material (3)
is unchanged. The above figure on the
right shows the “transformed” section. 3.
Next calculate the moment of inertia of the entire “transformed”
section about its neutral axis, y. Iyy =
2[ (1/12) b1h13 + b1h1(h1/2
+ h2 + h3/2)2 + (1/12) b2h23
+ b2h2(h2/2 + h3/2)2
] + (1/12) b3h33 where b1 = 18 in, h1
= 1 in, b2 = 9 in, h2
= 2 in, b3 = 6 in, h3
= 3 in Iyy = 2[
(1/12)(18)(13) + (18)(42) + (1/12)(9)(23) +
(18)(5/2)2 ] + (1/12)6(33) So for the “transformed”
section Iyy =
829.5 in4 4.
Now the bending stress in terms of material (3) can be calculated
using σ
= Mc/Iyy
. Click here to continue
with this example. |
| Return to Notes on Solid Mechanics |
|---|
All rights reserved.