MathHelp

The Chain Rule for Functions of Several Variables

In a Nut Shell: Recall that the chain rule for a function, y, of one independent variable,

x, was very important in that it enabled you to replace the derivative of a complicated

function with a product of simpler derivatives, called the “chain” rule.

Recall the Chain Rule: If u = u(x) and x = x(t), then du/dt = [du/dx][dx/dt]

Now consider a function, u(x,y) (which has continuous, first-order derivatives)

and that x = g(t) and y = h(t) are differentiable functions. Then u is a

differentiable function of t .

Terminology:

u is the dependent variable, x and y are intermediate variables

and t is the independent variable

Suppose u = u(x,y) has continuous first-order derivatives. Then

du/dt = [∂u/ ∂x] dx/dt + [∂u/ ∂y] dy/dt

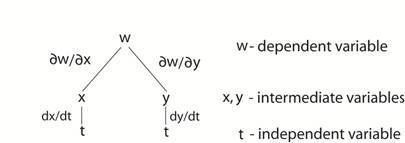
It can be helpful to construct a “tree diagram” to illustrate the chain rule structure.

Tree diagram for w = w(x,y) where x = x(t) and y = y(t).

It follows then that the chain rule for dw/dt is given as above by the expression:

dw/dt = [∂w/ ∂x] dx/dt + [∂w/ ∂y] dy/dt

Return to Calculus 3 Notes