Maxima and
Minima of Functions on a Closed Domain
|
In a Nut Shell: Maximum and minimum values of
functions hold special interest in calculus. Minimizing cost or maximizing profit
functions are two common applications. If satisfied, the following Extreme Value Theorem guarantees f(x) has
extreme values. If f(x) is continuous on a closed interval [a,b], then there exists numbers c and
d in [a,b] such that
f(c) is the minimum and
f(d) is the maximum value of f
on [a,b]. |
|
Click here to review the
first derivative test and the second derivative test. |
|
The maximum and minimum values of
y(x) on the curve of y(x)
are: Either at the “top” of
or at the “bottom” of the curve
the “slope” must be zero. So dy/dx = y’(x)
= 0 at either location c
or d; dy/dx is the slope of
the curve y(x) |
|
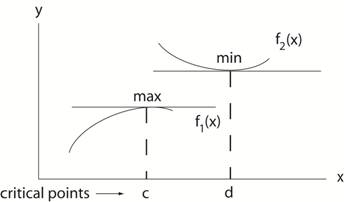
A location, x = c, where the slope of f(x) is zero i.e.
df(x)/dx| x =
c = 0 is called a critical point of f(x). Note: df(x)/dx| x = c
= 0, f ’(c)
= 0 (the slope is zero at the point x = c ) But
f ’(c) might not exist (vertical tangent to curve at x
= c ) |
|
The maximum or minimum values of
y(x) may take on local or
global values. Let D
be the domain on which y(x) is defined. Then at
x = c : f(c) is a global maximum if f(c) ≥ f(x) for all x in D f(c) is a global minimum if f(c) ≤ f(x) for all x in D In both cases df(x)/dx| x =c ,
f ’(c) = 0 |
| Return to Notes for Calculus 1 |
All rights reserved.