|
Strategy: Let
r = x i + y
j + z
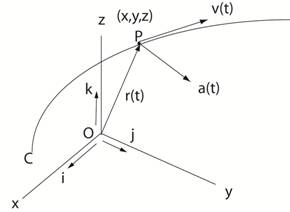
k be a position vector from the
origin, O, to an arbitrary
point P(x,y,z) (particle) on a curve, C, in space . Then
dr
/ dt is a vector tangent to
this curve. This curve, C, represents the path of
motion of the particle, P, in space.
Take the derivative
of the position vector, r , to obtain the velocity of the particle, v .
v
=
dr
/ dt
= velocity
of the particle along its path
So v =
dr
/ dt
= dx/dt i + dy/dt j + dz/dt k
where dx/dt, dy/dt, and
dz/dt represent the x, y, and z-components of
velocity
of the particle moving
along C.
|