Basics of Multiple Integrals and Applications Click here for Double Integrals

 

 

In a Nut Shell:  The integral under a curve, y(x), gives the area underneath the curve.

For a single integral, the differential area, dA, can be represented by  dA  =  y dx,  by 

dA  =  x dy. 

 

For double integrals the differential area, dA, can be represented by dA  =  dy dx or by

 dA  =  dx dy.  For areas using double integrals     A  =  ∫ ∫ dy dx  or  A  =  ∫ ∫ dx dy  . 

 

In a similar manner the volume, V,  between two surfaces leads to a triple integrals

V  =   ∫ ∫ ∫dx dy dz  =  ∫ ∫ ∫dx dz dy  or an combination of integration order.  Some

orders may be easier than others to carry out the integration.

 

 In all cases you need to determine the limits of integration.

 

 

 

 

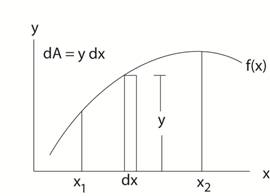
Recall that the total area under the curve, y = f(x), in Calculus 2 was given by:

 

                                          x2                      x2

                                   A = ∫  f(x) dx    =    ∫ y dx ------------------- (1)

                                          x1                     x1

 

The element of area, dA was visualized as a rectangle of width dx and height y

under the curve y = f(x). The total area then was the “sum” of each rectangle.

The region of integration extended from x1 to x2 .

                           

                       

 

Next consider the area between two curves y1 = f1 (x) and y2 = f2 (x) where

the curve for y2 lies above y1 . Using the approach in Calculus 2, the area between

the curves is: 

                        x2a

                A = ∫  (y2 - y1 ) dx ------------------------------------- (2)

                       x1a

 

where x1a and x2a are the x-coordinates of the points of intersection of the

two curves.

                              Click here to continue with this case.

 



Copyright © 2017 Richard C. Coddington

All rights reserved.