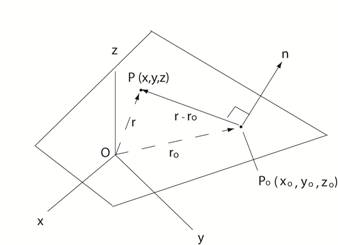
Planes in Space

In a Nut Shell: The equation of a plane is found by taking the dot product of any line

in the plane with its normal vector, n . The result is that the dot product is zero since the

normal vector is perpendicular to the arbitrary line in the plane.

Strategy: Let r = < x, y, z > be a vector from the origin, O, to an arbitrary point

P(x,y,z) in the plane. Let r_o = < x₀, y₀, z₀ > be a vector from the origin to the point

Po(x_o, y_o, z_o) also in the plane. So the vector r - r_o is a vector within the plane to

be determined. Let < i, j, k > be unit vectors along the x, y, and z axes.

The dot product of the vector r - r_o with the normal vector n ( n is normal to

every line in the plane) must equal zero since the vectors are perpendicular to each other.

( r - r_o ) ∙ n = 0

If n = a i + b j + c k , then the equation of the plane has the following form:

(x - x_o) a + (y - y_o) b + (z - z_o) c = 0

Note: The normal to a plane can be determined by taking the cross product of any

two non-parallel lines (vectors) in the plane.

Further note: The angle between any two intersecting planes can be determined by

finding the normal to each plane, say n₁ and n₂ , and then by finding the dot product

of these two vectors. Let θ be the angle between n₁ and n₂

cos θ = n₁ ∙ n₂ / | n₁ | | n₂ |

Click here for an example.

Return to Calculus 3 Notes

Copyright © 2017 Richard C. Coddington

All rights reserved.