Areas and Arc Lengths using Polar Coordinates

In a Nut Shell: Areas and arc lengths expressed in polar coordinates can be calculated

in much the same way as for Cartesian coordinates.

Strategy: For areas start with an expression for the element of area, dA = ½ r² dθ .

For arc lengths start with the expression for the differential arc length, dS where

dS = √ [ ( r² + (dr/dθ)² ] dθ . In both cases integrate over the region to get the total area

or total arc length.

In polar coordinates r = r(θ) where r is the radial distance to the point, P, on the curve

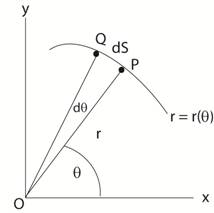
r = r(θ) and θ is the angle of the ray to the point, P, shown in the figure below.,

The element of area, dA, is the ”triangular” area of OPQ dA = ½ r² dθ

The element of arc length, dS, is the length along the arc, PQ.

From the Pythagorean Theorem dS = √ ( dx² + dy² ) . Convert to polar coordinates using

x = r cos θ , y = r sin θ [ remember r = r(θ) ] Use the “chain rule”.

dx = (dr/dθ) cos θ + r(θ) (- sin θ ) dθ and dy = (dr/dθ) sin θ + r(θ) cos θ dθ

so dS = √ [ ( r² + (dr/dθ)² ] dθ

θ = b

So the total area under the curve, r = r(θ) is A = ∫ ½ [ r(θ)² ] dθ

θ = a

θ = b

So the total arc length, L, L = ∫ √ [ ( r² + (dr/dθ)² ] dθ

θ = a

Click here for examples.

Return to Calculus 2 Notes Involving Sequences, Infinite Series, etc

Copyright © 2017 Richard C. Coddington

All rights reserved.