Integrals using Trig Substitutions

In a Nut Shell: Integrals, ∫ f(x) dx, where the integrand, f(x), has one of

the following forms ( note: the exponent can be to any power, p )

a. f(x) = ( a² – x² ) ^p where a is a constant

b. f(x) = ( a² + x² ) ^p where a is a constant

c. f(x) = ( x² – a² ) ^p where a is a constant

have convenient trig substitutions that lead to the evaluation of the integral.

For integrals involving f(x) = ( a² – x² ) ^p the trig substitution x = a sin θ

is helpful. In this case dx = a cos θ and ( a² – x² ) = a² cos² θ .

For integrals involving f(x) = ( a² + x² ) ^p the trig substitution x = a tan θ

is helpful. In this case dx = a sec² θ dθ and ( a² + x² ) = a² sec² θ .

For integrals involving f(x) = ( x² - a² ) ^p the trig substitution x = a sec θ

is helpful. In this case dx = a sec θ tan θ dθ and ( x² + a² ) = a² tan² θ .

The procedure is to make the substitution, then evaluate the integral in terms of the

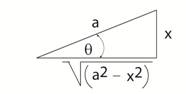
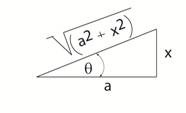
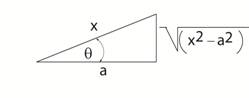
new variable, θ, and finally convert back into the original variable, x. This conversion

is best completed using the following diagrams. For case a (above) x = a sin θ

For case b (above) x = a tan θ

For case c (above) x = a sec θ

Click here for examples.

Return to Notes for Calculus 2

Copyright © 2017 Richard C. Coddington

All rights reserved.