Math Help

Volume of Revolution using Disks and Shells (click here for Method of Shells)

In a Nut Shell: There are two methods for calculating volumes of revolution - the method

of disks and the method of shells. Calculation of the volume generated by rotating a

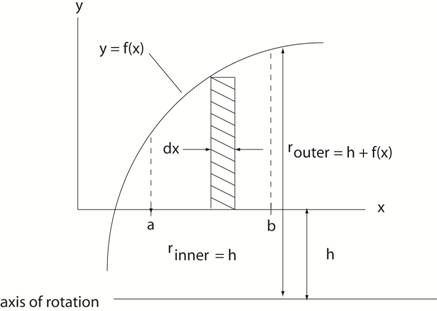
curve or a set of curves about a designated axis of rotation is a three step process such as:

For the Method of Disks

Step 1: Identify the element of volume, dV, and show it on the graph of y = f(x)

For a disk element dV = (πr²_outer – πr²_inner) dx. See figure below.

Step 2: Determine the limits of integration for the region (volume to be calculated)

Step 3: Evaluate the integral

Step 1

Region to be rotated is bounded by x = a, x = b, y = 0, and y = f(x).

Note that the disk (donut) is generated by

rotating the hatched area shown about the axis of rotation.

Steps 2 and 3

Establish limits of integration. In this case the integration is from x = a to x = b.

Express the total volume as an integral over the region rotated about the axis of

rotation. The disk is defined by dV = (πr²_outer – πr²_inner) dx or in this case

dV = [ π ( h+ f(x))² – π h²] dx .

x=b

V = ∫ [ π ( h+ f(x)² ) – π h²] dx

x=a