Centroids of Cross-Sectional Areas Click here for Moments of Inertia of Areas

Key Concepts: In solid mechanics properties of X˗ sectional areas including centroid and

moment of inertia are important. Centroids are frequently at the point of symmetry of

the X˗section such as at the center of a circular, annular, rectangular, or box X-section.

The centroid of a X˗sectional area is the idealized location where all its area can be thought to be concentrated. Again, to locate the centroid use the principle of first moments:

The moment of the sum equals the sum of the moments of individual parts.

In a Nutshell: Two common methods can be used to located the centroid – the method of integration and the method of summation for composite areas where individual areas are joined together. Note: If there is a void (i.e. a hole such as a circular area), then the void has a negative contribution.

For the method of integration: A y_cg = ʃ y dA and A z_cg = ʃ z dA

where A is the total area, y_cg is the y-coordinate of the centroid, z_cg is the z-coordinate of the

centroid, and (y,z) are the coordinates to the element of area, dA

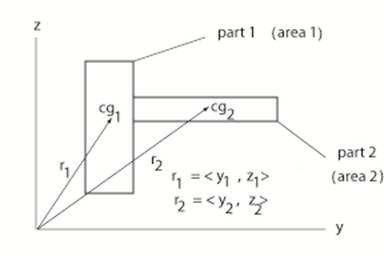
For the method of summation:

Areas can be combined together to form “composite sectional areas”. The principle of

first moments also applies to each “composite sectional area”. Use “summation” form.

For example: (Σ A_i )y_cg = Σ A_i y_i (Also, (Σ A_i )z_cg = Σ A_i z_i )

i.e. (area₁ + area₂) y_cg = (z₁ )area₁ + (y₂)area₂

So y_cg = [ (y₁ )area₁ + (y₂)area₂ ] / (area₁ + area₂)

where y_cg is the y-component of the centroid of the composite area

Click here for examples.

Return to Notes on Solid Mechanics

Copyright © 2019 Richard C. Coddington
All rights reserved.