Moment of Inertia Click here for the Parallel Axis Theorem

Key Concepts: The moment of inertia, I, is an important property of an area. It is the

"second" moment of an element of area about axes y and z (using integration) such as

(see figure below)

I_zz = ʃ y² dA I_yy = ʃ z² dA

The moment of inertia is frequently calculated about the centroidal axes of the X-section.

The parallel axis theorem then provides a convenient method to calculate the moment of

inertia about any parallel axes to the centroidal axes.

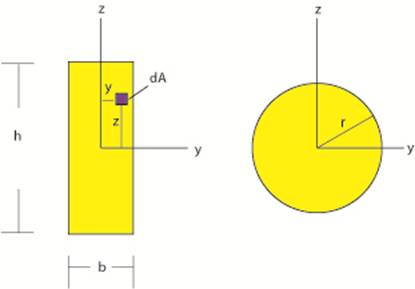
In a Nutshell: The analysis of stresses in beams uses the moment of inertia of area in its

calculation. Common X-sections include rectangular, box, tee, circular, and annular. The table

below contains the moments of inertia of areas for rectangular and circular X-sections.

I_yy I_zz

Rectangular Area	(1/12) bh^3	(1/12) hb^3
Circular Area	(1/4)π r^4	(1/4)π r^4

X-sections can be combined to form composite sections such as box sections, tee sections

annular sections, and channel sections. Use superposition to calculate the moment of inertia

of composite sections.

Click here for an example involving a channel section.

Return to Notes on Solid Mechanics

Copyright © 2019 Richard C. Coddington
All rights reserved.