Transformation of Stresses/Mohr’s Circle

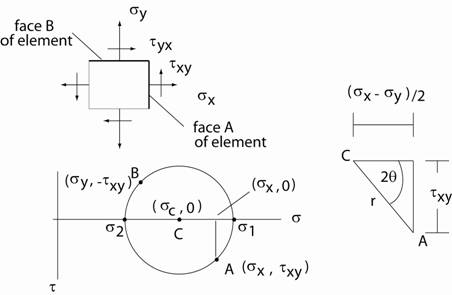
Construction of Mohr’s Circle starts with identifying “faces” on the element.

Each face of the element corresponds to a point on Mohr’s Circle. See the figure below.

A = a point on Mohr’s circle corresponding to “face A” on the element

B = a point on Mohr’s circle corresponding to “face B” on the element

C = center of the circle with coordinates ( σ_c , 0 )

Steps to Plot Mohr’s Circle

1. Locate the center of the circle σ_c = (σ_x + σ_y)/2 and t = 0
2. Determine the radius from geometry r = sqrt { [(σ_x - σ_y)/2]² + τ _xy² }
3. Note: tan 2θ = τ _xy / [(σ_x - σ_y )/2]

Sign convention on Mohr’s circle:

+ normal stresses indicate tension and - normal stresses indicate compression

+ shearing stresses are counterclockwise (CCW) and – shearing stresses are (CW)

Important points to note regarding Mohr’s Circle

1. A point on Mohr’s circle represents a face on the element.
2. Rotation of 2θ on Mohr’s circle yields a rotation of θ on the element

both in the same direction.

3. Faces on which there is no shear stress are the principal faces and give the maximum and minimum normal stresses (the principal stresses).
4. The radius of Mohr’s circle gives the maximum shearing stress.
5. A convenient check on your construction is: σ_x + σ_y = σ₁ + σ₂

where σ₁ and σ₂ are the principal stresses

Click here for examples.

Return to Notes on Solid Mechanics

Copyright © 2019 Richard C. Coddington
All rights reserved.