Engr Help

Mohr’s Circle - Stress

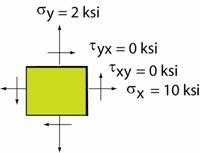
Example: The element shown below has the following stresses acting on its faces.

σ_x = 10 ksi, σ_y = 2 ksi, τ_xy = 0. Construct Mohr’s Circle. Determine the

maximum and minimum normal stresses and the maximum shear stress. Find the

angle of the plane on which the maximum shear stress acts.

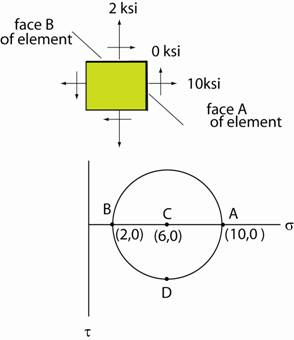
Strategy: Identify face A and face B on the element. Construct Mohr’s Circle. Rotate from

plane A to determine the angle of the plane on which the maximum shear stress occurs.

The center of the circle is at σ_C = (σ_x + σ_y)/2 = 10 + 2)/2 = 6 and τ_xy = 0.

So the radius of the circle is σ_A – σ_C = 4 ksi

Note: σ_max = 10 ksi, σ_min = 2 ksi, τ_max = radius = 4 ksi

The principal stresses σ₁ = 10 ksi, σ₂ = 2 ksi acting on face A and face B respectively.

The maximum shear stress, τ_max= 4 ksi occurs at D. So rotation from A to D on Mohr’s

circle is 90^o clockwise. Rotation on the element is half that. So the plane on which the

maximum shear stress occurs is 45^o clockwise from face A of the element shown above.

On face D on the element, σ_x = 6 ksi and τ_xy = 4 ksi. Click here to view this element.

Return to Notes on Solid Mechanics