Change of Variables in Integrals

In a Nut Shell: Sometimes the evaluation of a double integral over a region, R, is

difficult due to the complexity of the integrand, F(x,y), the shape of the region, R,

or both.

I = ∫ ∫ F(x,y) dx dy

R

In such cases, it may prove helpful to change the variables of integration from

(x,y) to (u,v) to simplify either the integrand, the region of integration, or both.

Recall change of variables (i.e. from rectangular to polar coordinates) was sometimes

helpful in evaluating single integrals.

Strategy: Find a transformation, called the Jacobian transformation, J_T(u,v), that simplifies

the integrand, the region of integration, R, or both. This is the hard part. There is no set

strategy. Two suggestions are to look at the integrand and pick a substitution that simplifies

it or look at the region of integration and again pick a substitution that simplifies it.

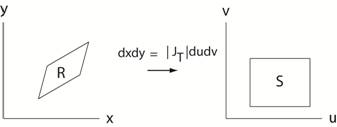
Consider regions, R, in the xy-plane that are parallelograms. Let dx dy be the original element

of area for region R and J_T(u,v) du dv be the rectangular element of area of the transformed

region, S, as shown in the figure below.

Then given sufficient continuity dx dy = | J_T(u,v) | du dv

where = J_T(u,v) = the Jacobian transformation defined as follows:

∂x/∂u ∂x∂v

J_T(u,v) = det where | J_T(u,v) | is the magnitude of the Jacobian

∂y/∂u ∂y∂v

and where det denotes the magnitude of the 2 x 2 determinant of the partial

derivatives. The integral then becomes:

I = ∫ ∫ F(x,y) dx dy =  ∫ ∫ G(u,v) | J_T(u,v) | du dv

R S

R is the original region of integration and S is the transformed region of integration.

Click here to continue with discussion.

Return to Calculus 3 Notes

Copyright © 2017 Richard C. Coddington

All rights reserved.