Math Help

Approximate Area using n rectangles -- The Riemann Sum

In a Nut Shell: Premise The area underneath the curve y = f(x) from x = a

to x = b can represented by a collection of small rectangular areas whose sum

approximates the area underneath the curve. There are three common sampling

points used to establish the area of each rectangle - - the right end point, the

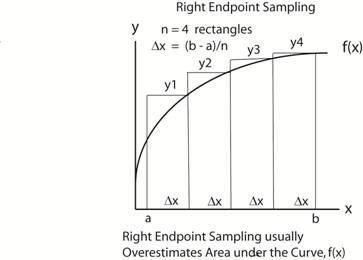
midpoint, and the left end point. The right end point option is illustrated below.

Procedure using right endpoints as the sampling points.

In general, break the area under the curve, y = f(x), for a ≤ x ≤ b

into n rectangles each of width Δx = ( b – a ) / n and xi* = a + i Δx

Let yi = f(x_i*) = y-value of the right endpoint for each individual rectangle.

The approximate total area is the finite Riemann sum of the n individual rectangles.

b n

ʃ f(x) dx = Σ f(x_i*) Δ x is called the Riemann Sum

a i = 1

For the figure below, the approximate total area is then = ( y1 + y2 + y3 + y4 ) Δx

The exact value of total area is:

b n

ʃ f(x) dx = lim ∑ f(xi*) Δ x

a n → ∞ i = 1