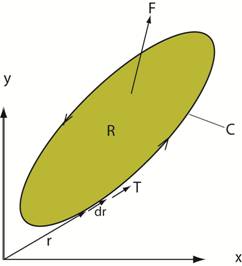
Stokes’ Theorem

Background: Recall that Green's theorem gives the relationship between a line

integral around a simple closed curve, C, in the x-y plane to a double integral over

the plane region R bounded by C. See the figure below.

In its “curl form”

Green’s Theorem is: ∫ F . dr = ∫ F . T ds = ∫ ∫ curl_z F dA

C C R

where

F = P(x,y) i + Q(x,y) j = the vector field

dr = dx i + dy j = T ds

T = the unit tangential vector to the path C

ds = the arc length along the curve, C

dA = the element of area in R

i j k

Note: curl_z F = ∂/∂x ∂/∂y ∂/∂z = [∂Q/∂x - ∂P/∂y] k

P(x,y) Q(x,y) 0

In other words, curl_z F is the z-component of curl F = curl F . k

Click here to move on to a discussion of Stokes’ Theorem.

Return to Calculus 3 Notes

Copyright © 2018 Richard C. Coddington

All rights reserved.