Surface Integrals (continued)

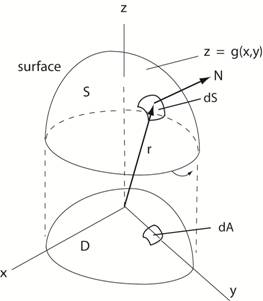
Also note the partial derivatives r_u = ∂ r / ∂ u and r_v = ∂ r / ∂ v

Now the element of surface area is dS = | r_u du x r_v dv | = | r_u x r_v | du dv

but r_u x r_v = N = normal to the surface, S and du dv = dA

So the relation between the element of surface area, dS, and the element of area, dA

is

dS = | N | dA (See the figure below)

Evaluation of the surface integral I_s = ∫ f(x, y, z) dS is a two-step process.

S

First write the integrand f(x,y,z) as a function of two independent variables.

i.e. If the surface is given by z = g(x,y), then f(x,y,z) = f(x, y, g(x,y))

Next write the element of surface area, dS, in terms of the area element, dA.

dS = | N(u,v)| du dv = | N(u,v)| dA where N(u,v) = ∂r/∂u x ∂r/∂v

take u = x and v = y so N(x,y) = ∂r/∂x x ∂r/∂y

Here N(x,y) represents the normal vector to the surface, S, at each arbitrary

point (x,y,z) and r = xi + yj + g(x,y)k is the position vector from the origin of the

coordinate system to any arbitrary point (x,y,z) on the surface, S. See the figure below.

Click here to continue discussion of surface integrals.

Return to Calculus 3 Notes

Copyright © 2017 Richard C. Coddington

All rights reserved.